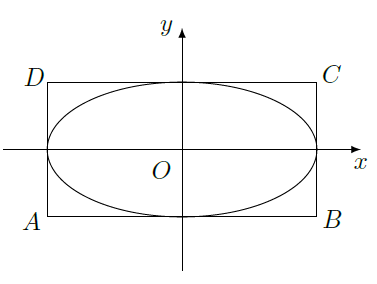
如图,椭圆
的离心率为
,直线
和
所围成的矩形
的面积为8.
(Ⅰ)求椭圆
的标准方程;
(Ⅱ) 设直线
与椭圆
有两个不同的交点
与矩形
有两个不同的交点
.求
的最大值及取得最大值时
的值.
推荐套卷
如图,椭圆
的离心率为
,直线
和
所围成的矩形
的面积为8.

(Ⅰ)求椭圆
的标准方程;
(Ⅱ) 设直线
与椭圆
有两个不同的交点
与矩形
有两个不同的交点
.求
的最大值及取得最大值时
的值.