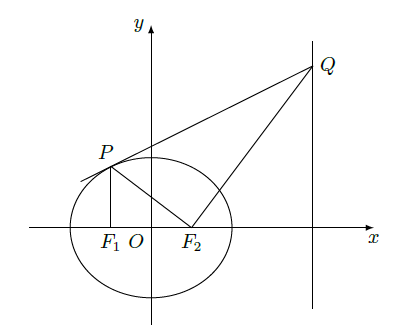
如图,
分别是椭圆
的左,右焦点,过点
作
轴的垂线交椭圆的上半部分于点P,过点
作直线
的垂线交直线
于点
;
(I)若点
的坐标为(4,4);求椭圆
的方程;
(II)证明:直线
与椭圆
只有一个交点
.
推荐套卷
如图,
分别是椭圆
的左,右焦点,过点
作
轴的垂线交椭圆的上半部分于点P,过点
作直线
的垂线交直线
于点
;

(I)若点
的坐标为(4,4);求椭圆
的方程;
(II)证明:直线
与椭圆
只有一个交点
.