（本小题满分14分）
已知函数
．
（1）求函数
的最小值；
（2）证明：对任意
恒成立；
（3）对于函数
图象上的不同两点
，如果在函数图象上存在点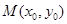
（其中
）使得点
处的切线
，则称直线
存在“伴侣切线”．特别地，当
时，又称直线存在 “中值伴侣切线”．试问：当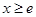
时，对于函数
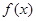图象上不同两点
、
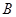，直线是否存在“中值伴侣切线”？证明你的结论．
对任意
的整数恒成立，求实数
的取值范围；
，
的前
项和为
，求证：
设过点
且不与坐标轴垂直的直线交椭圆于
两点，线段
的垂直平分线与x轴交于
，求点
元）推荐套卷
（本小题满分14分）
已知函数．
（1）求函数的最小值；
（2）证明：对任意恒成立；
（3）对于函数图象上的不同两点，如果在函数图象上存在点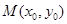（其中）使得点处的切线，则称直线存在“伴侣切线”．特别地，当时，又称直线存在 “中值伴侣切线”．试问：当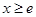时，对于函数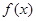图象上不同两点、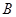，直线是否存在“中值伴侣切线”？证明你的结论．
粤公网安备 44130202000953号