某企业投资1千万元于一个高科技项目,每年可获利25%.由于企业间竞争激烈,每年底需要从利润中取出资金
万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.设经过
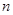年后该项目的资金为
万元.
1)写出数列
的前三项
,并猜想写出通项.
2)求经过多少年后，该项目的资金可以达到或超过
千万元.
相关试题
的定义域为
，函数
的定义域；
的解集.
的离心率为
，长轴长为
，直线
交椭圆于不同的
两点.
是坐标原点，求
面积的最大值.
中
,
边上的中线
所在直线方程为
,
的平分线方程
为
.
的坐标；
的方程.
轴相切，圆心在直线
上，且被直线
截得的弦长为
的圆的方程．
经过直线
的交点，且点
到直线推荐套卷
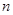某企业投资1千万元于一个高科技项目,每年可获利25%.由于企业间竞争激烈,每年底需要从利润中取出资金万元进行科研、技术改造与广告投入,方能保持原有的利润增长率.设经过年后该项目的资金为万元.
1)写出数列的前三项,并猜想写出通项.
2)求经过多少年后，该项目的资金可以达到或超过千万元.
粤公网安备 44130202000953号