如图，一个小球从M处投入，通过管道自上而下落A或B或C。已知小球从每个叉口落入左右两个 管道的可能性是相等的．某商家按上述投球方式进行促销活动，若投入的小球落到A，B，C，则分别设为l，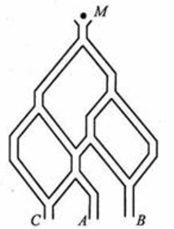
2，3等奖．（I）已知获得l，2，3等奖的折扣率分别为50％，70％，90％．记随变量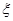
为获得k(k=1,2,3)等奖的折扣率，求随机变量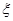的分布列及期望
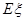；(II)若有3人次(投入l球为l人次)参加促销活动，记随机变量
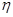为获得1等奖或2等奖的人次，求
．
相关试题
已知函数
．
（Ⅰ）求证：不论a为何实数f（x）在（﹣∞，+∞）上为增函数；
（Ⅱ）若f（x）为奇函数，求a的值；
（Ⅲ）在（Ⅱ）的条件下，求f（x）在区间[1，5）上的最小值．
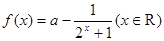是定义在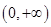
内的增函数，且满足
．
；
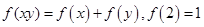的解集．
2≤x≤8．
，求y关于t的函数关系式，并写出t的范围；
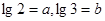，试用
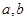表示
．
，求a的取值范围．相关知识点
推荐套卷
粤公网安备 44130202000953号