(本小题满分15分)
(Ⅰ)如图1,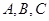 是平面内的三个点,且
是平面内的三个点,且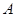 与
与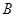 不重合,
不重合,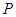 是平面内任意一点,若点
是平面内任意一点,若点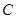 在直线
在直线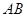 上,试证明:存在实数
上,试证明:存在实数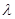 ,使得:
,使得: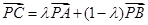 .
.
(Ⅱ)如图2,设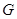 为
为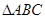 的重心,
的重心,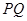 过
过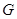 点且与
点且与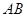 、
、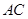 (或其延长线)分别交于
(或其延长线)分别交于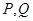 点,若
点,若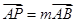 ,
,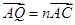 ,试探究:
,试探究: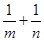 的值是否为定值,若为定值,求出这个定值;若不是定值,请说明理由.
的值是否为定值,若为定值,求出这个定值;若不是定值,请说明理由.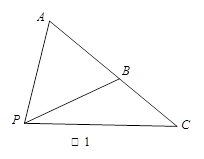

相关知识点
推荐套卷
(本小题满分15分)
(Ⅰ)如图1,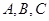 是平面内的三个点,且
是平面内的三个点,且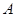 与
与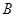 不重合,
不重合,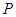 是平面内任意一点,若点
是平面内任意一点,若点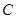 在直线
在直线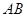 上,试证明:存在实数
上,试证明:存在实数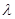 ,使得:
,使得: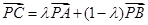 .
.
(Ⅱ)如图2,设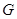 为
为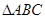 的重心,
的重心,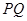 过
过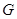 点且与
点且与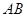 、
、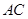 (或其延长线)分别交于
(或其延长线)分别交于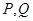 点,若
点,若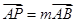 ,
,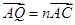 ,试探究:
,试探究: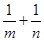 的值是否为定值,若为定值,求出这个定值;若不是定值,请说明理由.
的值是否为定值,若为定值,求出这个定值;若不是定值,请说明理由.
