如图,平面直角坐标系中,射线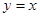 (
(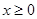 )和
)和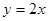 (
(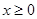 )上分别依次有点
)上分别依次有点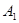 、
、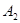 ,……,
,……,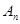 ,……,和点
,……,和点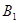 ,
,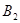 ,……,
,……,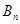 ……,其中
……,其中 ,
,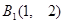 ,
,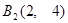 .且
.且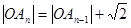 ,
, 
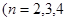 ……).
……).
(1)用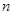 表示
表示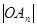 及点
及点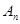 的坐标;
的坐标;
(2)用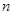 表示
表示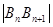 及点
及点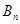 的坐标;
的坐标;
(3)写出四边形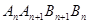 的面积关于
的面积关于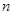 的表达式
的表达式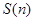 ,并求
,并求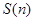 的最大值.
的最大值.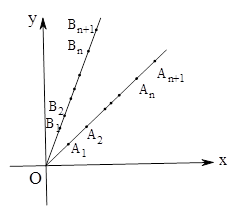
相关知识点
推荐套卷
如图,平面直角坐标系中,射线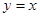 (
(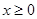 )和
)和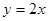 (
(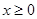 )上分别依次有点
)上分别依次有点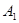 、
、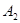 ,……,
,……,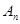 ,……,和点
,……,和点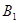 ,
,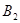 ,……,
,……,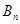 ……,其中
……,其中 ,
,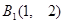 ,
,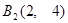 .且
.且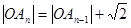 ,
, 
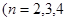 ……).
……).
(1)用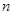 表示
表示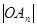 及点
及点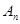 的坐标;
的坐标;
(2)用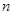 表示
表示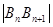 及点
及点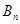 的坐标;
的坐标;
(3)写出四边形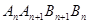 的面积关于
的面积关于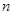 的表达式
的表达式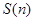 ,并求
,并求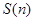 的最大值.
的最大值.