在平面直角坐标系
中,
是抛物线
的焦点,
是抛物线
上位于第一象限内的任意一点,过
三点的圆的圆心为
,点
到抛物线
的准线的距离为
.
(Ⅰ)求抛物线
的方程;
(Ⅱ)是否存在点
,使得直线
与抛物线
相切于点
?若存在,求出点
的坐标;若不存在,说明理由;
(Ⅲ)若点
的横坐标为
,直线
与抛物线
有两个不同的交点
,
与圆
有两个不同的交点
,求当
时,
的最小值.
相关知识点
推荐套卷
 、
、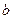 、
、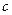 分别是
分别是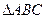 的三个内角
的三个内角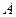 、
、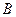 、
、 所对的边;
所对的边;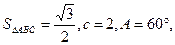 求
求 ,且
,且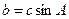 ,试判断
,试判断 中,
中,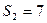 ,
,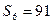 ,求
,求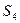 .
. ,
,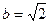 ,B=45°求A、C及c (结论保留最简根式形式)
,B=45°求A、C及c (结论保留最简根式形式)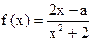 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数. 的集合A;
的集合A; 的两实数根为x1、x2,试问:是否存在实数m,使得不等式
的两实数根为x1、x2,试问:是否存在实数m,使得不等式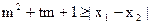 对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由? 0), 且点P使
0), 且点P使 成公差小于零的等差数列.
成公差小于零的等差数列. ,
, 的夹角, 求
的夹角, 求
 粤公网安备 44130202000953号
粤公网安备 44130202000953号