在参加市里主办的科技知识竞赛的学生中随机选取了40名学生的成绩作为样本,这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组,成绩大于等于40分且小于50分;第二组,成绩大于等于50分且小于60分;……第六组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.在选取的40名学生中,
( I )求成绩在区间[80,90)内的学生人数;
(Ⅱ)从成绩大于等于80分的学生中随机选2名学生,求至少有1名学生成绩在区间[90,100] 内的概率。
相关知识点
推荐套卷
 x+y-2
x+y-2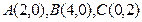 ,求这个圆的方程
,求这个圆的方程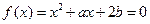 的一个根在(0,1)内,另一个根在(1,2)内,求:
的一个根在(0,1)内,另一个根在(1,2)内,求: 的值域;
的值域; 的值域;
的值域;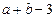 的值域.
的值域. 的顶点A为(3,-1),AB边上的中线所在直线方程为
的顶点A为(3,-1),AB边上的中线所在直线方程为 ,
, 的平分线所在直线方程为
的平分线所在直线方程为 ,求BC边所在直线的方程.
,求BC边所在直线的方程. 按向量a=(-1,2)平移后得到⊙O,直线l与⊙O相交于A、B两点,若在⊙O上存在点C,使
按向量a=(-1,2)平移后得到⊙O,直线l与⊙O相交于A、B两点,若在⊙O上存在点C,使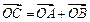 =λa,求直线l的方程及对应的点C的坐标.
=λa,求直线l的方程及对应的点C的坐标. 粤公网安备 44130202000953号
粤公网安备 44130202000953号