如图,在矩形ABCD中,AB=12cm,BC=8cm,点E,F,G分别从点A,B,C三点同时出发,沿矩形的边按逆时针方向移动,点E,G的速度均为2cm/s,点F的速度为4cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t秒时,△EFG的面积为S(cm2).当t=1秒时,S的值是多少?
写出S和t之间的函数解析式,并指出自变量t的取值范围.
若点F在矩形的边BC上移动,当t为何值时,以点E,B,F为顶点的三角形与以F,C,G为顶点的三角形相似?请说明理由.

相关知识点
推荐套卷
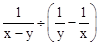 ,其中
,其中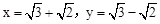 .
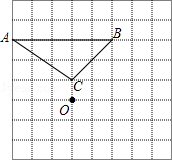
. ),C(1,
),C(1,
 (元)与国内销售数量
(元)与国内销售数量 (千件)的关系为:
(千件)的关系为: 若在国外销售,平均每件产品的利润
若在国外销售,平均每件产品的利润 (元)与国外的销售数量t(千件)的关系为:
(元)与国外的销售数量t(千件)的关系为:
 粤公网安备 44130202000953号
粤公网安备 44130202000953号