（本小题满分12分）
设平面向量
＝ （ m , -1）, 
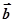=" (" 2 , n )，其中 m， n
{-2,-1,1,2}．
（1）记“使得//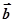成立的（ m，n）”为事件A，求事件A发生的概率；
（2）记“使得⊥（-2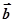）成立的（ m，n）”为事件B，求事件B发生的概率.
的定义域为
，且
时，
时，
．
，解答下述问题：
的取值范围；
，求实数
，集合
．
时，求
；
，求实数
的取值范围；
，求实数
；
，集合
，集合
；
，求实数
的取值范围；推荐套卷
（本小题满分12分）
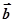设平面向量＝ （ m , -1）, =" (" 2 , n )，其中 m， n{-2,-1,1,2}．
（1）记“使得//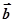成立的（ m，n）”为事件A，求事件A发生的概率；
（2）记“使得⊥（-2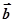）成立的（ m，n）”为事件B，求事件B发生的概率.
粤公网安备 44130202000953号