已知矩形纸片ABCD中,AB=24厘米,BC=10厘米.
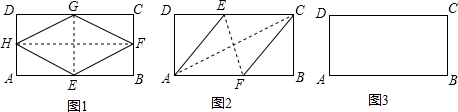
(1)按如下操作:先将矩形纸片上下对折,而后左右对折,再沿对角线对折,而后展开得到图中的折痕四边形EFGH(如图1),求菱形EFGH的面积.
(2)如图2,将矩形纸片ABCD折叠,使点A与点C重合得折痕EF,则四边形AECF必为菱形,请加以证明.
(3)请通过一定的操作,构造一个菱形EFGH(不同于第(1)题中的特殊图形),使菱形的四个顶点分别落在矩形ABCD的四条边上(E、F、G、H分别在边AB、BC、CD、DA上,且不与矩形ABCD的顶点重合).
①请简述操作的方法,并在图3中画出菱形EFGH.
②求菱形EFGH的面积的取值范围.