如图(1),分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA所在直线为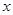 轴、
轴、 轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在
轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在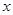 轴上)交y轴于另一点Q,抛物线
轴上)交y轴于另一点Q,抛物线 经过A、C两点,与
经过A、C两点,与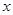 轴的另一交点为G,M是FG的中点,B点坐标为(2,2).
轴的另一交点为G,M是FG的中点,B点坐标为(2,2).求抛物线的函数解析式和点E的坐标;
求证:ME是⊙P的切线;

相关知识点
推荐套卷
如图(1),分别以两个彼此相邻的正方形OABC与CDEF的边OC、OA所在直线为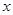 轴、
轴、 轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在
轴建立平面直角坐标系(O、C、F三点在x轴正半轴上).若⊙P过A、B、E三点(圆心在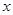 轴上)交y轴于另一点Q,抛物线
轴上)交y轴于另一点Q,抛物线 经过A、C两点,与
经过A、C两点,与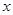 轴的另一交点为G,M是FG的中点,B点坐标为(2,2).
轴的另一交点为G,M是FG的中点,B点坐标为(2,2).求抛物线的函数解析式和点E的坐标;
求证:ME是⊙P的切线;
