已知两个全等的直角三角形纸片ABC、DEF，如图⑴放置，点B、D重合，点F在BC上，AB与EF交于点G．∠C＝∠EFB＝90°，∠E＝∠ABC＝30°，AB＝DE＝4．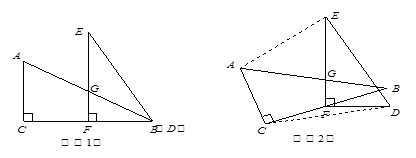
求证：△EGB是等腰三角形；
若纸片DEF不动，问△ABC绕点F逆时针旋转最小 度时，四边形ACDE成为以ED为底的梯形（如图⑵）．求此梯形的高
相关知识点
推荐套卷
已知两个全等的直角三角形纸片ABC、DEF，如图⑴放置，点B、D重合，点F在BC上，AB与EF交于点G．∠C＝∠EFB＝90°，∠E＝∠ABC＝30°，AB＝DE＝4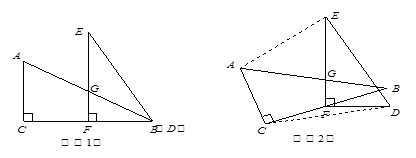．求证：△EGB是等腰三角形；
若纸片DEF不动，问△ABC绕点F逆时针旋转最小 度时，四边形ACDE成为以ED为底的梯形（如图⑵）．求此梯形的高
粤公网安备 44130202000953号