有两个可以自由转动的均匀转盘 ,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
,都被分成了3等份,并在每份内均标有数字,如图所示.规则如下:
①分别转动转盘 ;
;
②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等份线上,那么重转一次,直到指针指向某一份为止).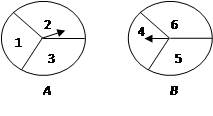
用列表法或树状图分别求出数字之积为3的倍数和数字之积为5的倍数的概率;
小明和小亮想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小明得2分;数字之积为5的倍数时,小亮得3分.这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏对双方公平.
相关知识点
推荐套卷



 (万元)与其销售量x(万盒)之间的函数关系式,并指出x的取值范围;
(万元)与其销售量x(万盒)之间的函数关系式,并指出x的取值范围;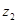 (万元)与卖给茶叶经销商的销售量x(万盒)之间的函数关系式,并指出x的取值范围;
(万元)与卖给茶叶经销商的销售量x(万盒)之间的函数关系式,并指出x的取值范围;
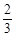 ,tan∠AEC=
,tan∠AEC=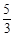 ,求圆的直径.
,求圆的直径.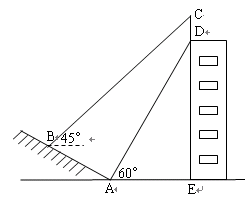

 粤公网安备 44130202000953号
粤公网安备 44130202000953号