如图,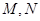 是抛物线
是抛物线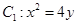 上的两动点(
上的两动点(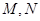 异于原点
异于原点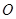 ),且
),且 的角平分线垂直于
的角平分线垂直于 轴,直线
轴,直线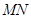 与
与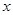 轴,
轴, 轴分别相交于
轴分别相交于 .
.
(1) 求实数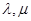 的值,使得
的值,使得 ;
;
(2)若中心在原点,焦点在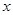 轴上的椭圆
轴上的椭圆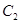 经过
经过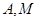 . 求椭圆
. 求椭圆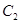 焦距的最大值及此时
焦距的最大值及此时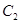 的方程.
的方程.
推荐套卷
如图,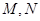 是抛物线
是抛物线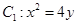 上的两动点(
上的两动点(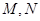 异于原点
异于原点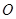 ),且
),且 的角平分线垂直于
的角平分线垂直于 轴,直线
轴,直线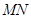 与
与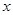 轴,
轴, 轴分别相交于
轴分别相交于 .
.
(1) 求实数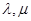 的值,使得
的值,使得 ;
;
(2)若中心在原点,焦点在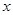 轴上的椭圆
轴上的椭圆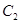 经过
经过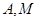 . 求椭圆
. 求椭圆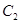 焦距的最大值及此时
焦距的最大值及此时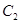 的方程.
的方程.