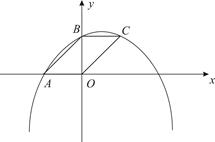
如图,已知抛物线y=-x2+bx+c与x轴负半轴交于点A,与y轴正半轴交于点B,且OA=OB.求b+c的值
若点C在抛物线上,且四边形OABC是平行四边形,试求抛物线的解析式;
在(2)的条件下,作∠OBC的角平分线,与抛物线交于点P,求点P的坐标.
相关知识点
推荐套卷
如图,已知抛物线y=-x2+bx+c与x轴负半轴交于点A,与y轴正半轴交于点B,且OA=OB.求b+c的值
若点C在抛物线上,且四边形OABC是平行四边形,试求抛物线的解析式;
在(2)的条件下,作∠OBC的角平分线,与抛物线交于点P,求点P的坐标.
