已知直线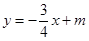 与
与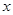 轴
轴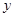 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6)求的
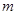 值和点A的坐标;
值和点A的坐标;在矩形OACB中,某动点P从点B出发以每秒1个单位的速度沿折线B-C-A运动.运动至点A停止.直线PD⊥AB于点D,与
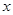 轴交于点E.设在矩形OACB中直线PD未扫过的面积为S,运动时间为 t.
轴交于点E.设在矩形OACB中直线PD未扫过的面积为S,运动时间为 t.
①求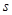 与t的函数关系式;
与t的函数关系式;
②⊙Q是△OAB的内切圆,问:t为何值时,PE与⊙Q相交的弦长为2.4 ?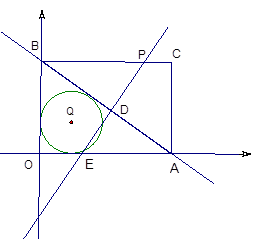
相关知识点
推荐套卷
已知直线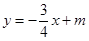 与
与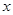 轴
轴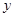 轴分别交于点A和点B,点B的坐标为(0,6)
轴分别交于点A和点B,点B的坐标为(0,6)求的
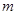 值和点A的坐标;
值和点A的坐标;在矩形OACB中,某动点P从点B出发以每秒1个单位的速度沿折线B-C-A运动.运动至点A停止.直线PD⊥AB于点D,与
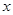 轴交于点E.设在矩形OACB中直线PD未扫过的面积为S,运动时间为 t.
轴交于点E.设在矩形OACB中直线PD未扫过的面积为S,运动时间为 t.
①求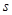 与t的函数关系式;
与t的函数关系式;
②⊙Q是△OAB的内切圆,问:t为何值时,PE与⊙Q相交的弦长为2.4 ?