在不透明的口袋中，有四只形状、大小完全相同的小球，四只小球上分别标有数字1，2，3，4. 小明先从盒子里随机取出一只小球(不放回)，记下数字作为平面直角坐标系内点的横坐标；再由小华随机取出一只小球，记下数字作为平面直角坐标系内点的纵坐标.用列表法或画树状图，表示所有这些点的坐标；
小刚为小明、小华两人设计了一个游戏：当上述（1）中的点在正比例函数y=2x-1图象上方时小明获胜，否则小华获胜. 你认为这个游戏公平吗？请说明理由.
如图，在测量塔高AB时，选择与塔底在同一水平面的同一直线上的C、D两点，用测角仪器测得塔顶A的仰角分别是30°和60°．已知测角仪器高CE=1.5米，CD=30米，求塔高AB．（保留根号）
如图，在平面直角坐标系xOy中，抛物线
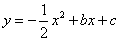与x轴交于A（1，0）、B（5，0）两点．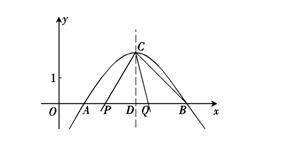
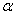(1). 求抛物线的解析式和顶点C的坐标；
(2). 设抛物线的对称轴与x轴交于点D，将∠DCB绕点C按顺时针方向旋转，角的两边CD和CB与x轴分别交于点P、Q，设旋转角为
（0°＜＜90°)
①当等于多少度时，△CPQ是等腰三角形？
②设
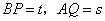，求s与t之间的函数关系式．
建设新农村，农村大变样.向阳村建起了天然气供应站，气站根据实际情况，每天从零点开始至凌晨4点，只打开进气阀，在以后的16小时(4∶00-20∶00)，同时打开进气阀和供气阀，20∶00-24∶00只打开供气阀，已知气站每小时进气量和供气量是一定的，下图反映了某天储气量
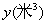与
(小时)之间的关系.
(1). 求0∶00-20∶00之间气站每小时增加的储气量；
(2). 求20∶00-24∶00时，
与的函数关系式，并画出函数图象；
(3). 照此规律运行，从这天零点起三昼夜内，经过＿＿小时气站储气量达到最大？最大值为＿＿＿
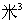.（请把答案直接写在在横线上，不必写过程）
如图,方形ABCD的AB边为直径，在正方形内部作半圆，圆心为O，DF切半圆于点E，交AB的延长线于点F，BF=4．求：
(1). cos∠F的值；
(2). BE的长．
粤公网安备 44130202000953号