如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(-2,0),B(-1, -3).
(1)求抛物线的解析式;
(2)点M为y轴上任意一点,当点M到A、B两点的距离之和为最小时,求此时点M的坐标;
(3)在第(2)问的结论下,抛物线上的点P使S△PAD=4S△ABM成立,求点P的坐标. 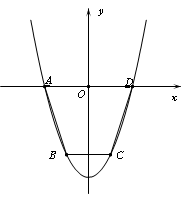
相关知识点
推荐套卷
如图,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(-2,0),B(-1, -3).
(1)求抛物线的解析式;
(2)点M为y轴上任意一点,当点M到A、B两点的距离之和为最小时,求此时点M的坐标;
(3)在第(2)问的结论下,抛物线上的点P使S△PAD=4S△ABM成立,求点P的坐标. 