阅读下面的材料，并解答问题：
材料：已知当a、b是正数时，有下列命题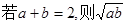
≤1
≤
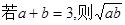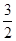
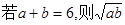≤ 3
（1）根据以上三个命题所提供的规律猜想：
≤ ；
（2）以上规律可用字母表示为 ；
（3）建造一个容积为8立方米，深2米的长方形无盖水池，池底和池壁的造价分别为每平方米120元和80元. 设池底的长为x米，水池总造价为y元，应用上述的规律，求水池的最低造价.
的值是正整数，求整数a．
．
．
，
，…
，试说明此猜想的正确性．（供参考：x3+y3=（x+y）（x2﹣xy+y2））
．相关知识点
推荐套卷
阅读下面的材料，并解答问题：
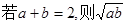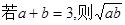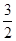
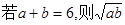材料：已知当a、b是正数时，有下列命题≤1≤≤ 3
（1）根据以上三个命题所提供的规律猜想：≤ ；
（2）以上规律可用字母表示为 ；
（3）建造一个容积为8立方米，深2米的长方形无盖水池，池底和池壁的造价分别为每平方米120元和80元. 设池底的长为x米，水池总造价为y元，应用上述的规律，求水池的最低造价.
粤公网安备 44130202000953号