如图,大正方形是由两个小正方形和两个长方形拼成的.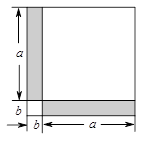
请你用两个不同形式的代数式表示这个大正方形的面积
由(1)可得到关于
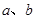 的等式,利用得到的这个等式计算:
的等式,利用得到的这个等式计算:
4.3232+2×4.323×0.677+0.6772.
相关知识点
推荐套卷
如图,大正方形是由两个小正方形和两个长方形拼成的.
请你用两个不同形式的代数式表示这个大正方形的面积
由(1)可得到关于
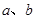 的等式,利用得到的这个等式计算:
的等式,利用得到的这个等式计算:
4.3232+2×4.323×0.677+0.6772.