如图,已知二次函数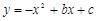 的图象经过A(
的图象经过A(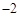 ,
,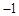 ),B(0,7)两点.
),B(0,7)两点.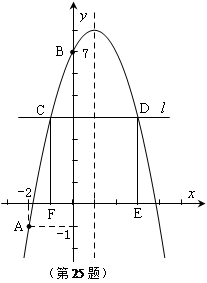
⑴求该抛物线的解析式及对称轴;
⑵当 为何值时,
为何值时,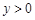 ?
?
⑶在 轴上方作平行于
轴上方作平行于 轴的直线
轴的直线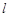 ,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作
,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作 轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.
轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.
相关知识点
推荐套卷
如图,已知二次函数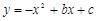 的图象经过A(
的图象经过A(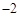 ,
,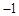 ),B(0,7)两点.
),B(0,7)两点.
⑴求该抛物线的解析式及对称轴;
⑵当 为何值时,
为何值时,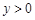 ?
?
⑶在 轴上方作平行于
轴上方作平行于 轴的直线
轴的直线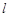 ,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作
,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作 轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.
轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.