在△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕顶点C顺时针旋转，旋转角为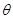
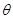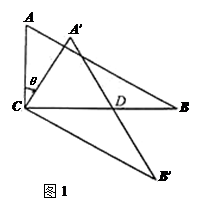
（0°＜＜180°），得到△A′B′C．如图（1），当AB∥CB′时，设A′B′与CB相交于点D．证明：△A′CD是等边三角形；
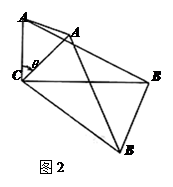
如图（2），连接A′A、B′B，设△ACA′ 和△BCB′ 的面积分别为S△ACA′ 和S△BCB′．求证：S△ACA′ ：S△BCB′ =1：3；
相关试题
与
是邻补角，OD、OE分别是
与直线
相交于A、B两点．第一象限上的点M（m，n）（在A点左侧）是双曲线
相关知识点
推荐套卷
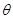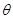在△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕顶点C顺时针旋转，旋转角为（0°＜＜180°），得到△A′B′C．如图（1），当AB∥CB′时，设A′B′与CB相交于点D．证明：△A′CD是等边三角形；
如图（2），连接A′A、B′B，设△ACA′ 和△BCB′ 的面积分别为S△ACA′ 和S△BCB′．求证：S△ACA′ ：S△BCB′ =1：3；
粤公网安备 44130202000953号