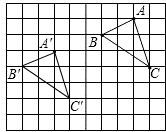
在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示，现将△ABC平移，使点A变换为点A′，点B′、C′分别是B、C的对应点．请画出平移后的△A′B′C′．并求△A′B′C′的面积．
若连接AA′，CC′，则这两条线段之间的关系是________．
相关试题
（m-2）-n（2-m）；（2）2a
-4a
；（2）（2a）3b4÷12a3b2
相关知识点
推荐套卷
在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示，现将△ABC平移，使点A变换为点A′，点B′、C′分别是B、C的对应点．请画出平移后的△A′B′C′．并求△A′B′C′的面积．
若连接AA′，CC′，则这两条线段之间的关系是________．
粤公网安备 44130202000953号