已知中心在原点,焦点在x轴上的椭圆离心率为
,且经过点
,过椭圆的左焦点作直线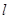
交椭圆于A、B两点，以OA、OB为邻边作平行四边形OAPB。
（1）求椭圆E的方程
（2）现将椭圆E上的点的纵坐标保持不变，横坐标变为原来的一半，求所得曲线的焦点坐标和离心率
（3）是否存在直线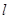，使得四边形OAPB为矩形？若存在，求出直线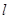的方程。若不存在，说明理由。
相关试题
设
， 
，
，若
图象中相邻的两条对称轴间的距离等于
．
的值；
中，
分别为角
的对边，
．当
时，求
的值．
.
.
,对于整数
.证明
；
。
的图象与
轴有交点为
，
的图象与
。设
，求证：
的图象与
与
之间。
方程
的两个实根为
，且满足
，设
，求证：
。
满足
，并且
（
为非零参数，
）
成等比数列，求参数
，常数
且
，证明：
推荐套卷
已知中心在原点,焦点在x轴上的椭圆离心率为,且经过点,过椭圆的左焦点作直线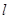交椭圆于A、B两点，以OA、OB为邻边作平行四边形OAPB。
（1）求椭圆E的方程
（2）现将椭圆E上的点的纵坐标保持不变，横坐标变为原来的一半，求所得曲线的焦点坐标和离心率
（3）是否存在直线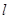，使得四边形OAPB为矩形？若存在，求出直线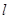的方程。若不存在，说明理由。
粤公网安备 44130202000953号