如图,抛物线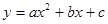 经过点A
经过点A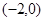 、B
、B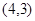 两点,且当x=3和x=-3时,这条抛物线上对应点的纵坐标相等,经过点C
两点,且当x=3和x=-3时,这条抛物线上对应点的纵坐标相等,经过点C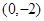 的直线
的直线 与x轴平行.
与x轴平行.
(1)求这条抛物线的解析式;
(2)若D是直线 上的一个动点,求使△DAB的周长最小时点D的坐标;
上的一个动点,求使△DAB的周长最小时点D的坐标;
(3)以这条抛物线上的任意一点P为圆心,PO的长为半径作⊙P,试判断⊙P与直线 的位置关系,并说明理由.
的位置关系,并说明理由.
相关知识点
推荐套卷
如图,抛物线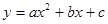 经过点A
经过点A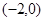 、B
、B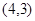 两点,且当x=3和x=-3时,这条抛物线上对应点的纵坐标相等,经过点C
两点,且当x=3和x=-3时,这条抛物线上对应点的纵坐标相等,经过点C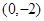 的直线
的直线 与x轴平行.
与x轴平行.
(1)求这条抛物线的解析式;
(2)若D是直线 上的一个动点,求使△DAB的周长最小时点D的坐标;
上的一个动点,求使△DAB的周长最小时点D的坐标;
(3)以这条抛物线上的任意一点P为圆心,PO的长为半径作⊙P,试判断⊙P与直线 的位置关系,并说明理由.
的位置关系,并说明理由.