如图，已知AB∥CD，分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系，并从所得的四个关系中任选一个加以说明，证明所探究的结论的正确性.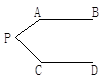
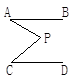
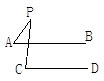
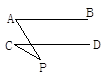
结论（1）____________________________；（2）____________________________；
（3）____________________________；（4）____________________________；
选择结论________，说明理由是什么.
相关试题
如图，已知AB∥CD，分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系，并从所得的四个关系中任选一个加以说明，证明所探究的结论的正确性.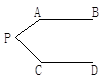
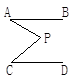
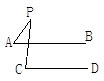
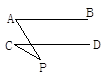
结论（1）____________________________；（2）____________________________；
（3）____________________________；（4）____________________________；
选择结论________，说明理由是什么.
，y为负数，求m的取值范围．
的值．
粤公网安备 44130202000953号