某种规格小纸杯的侧面是由一半径为18cm、圆心角是60°的扇形OAB剪去一半径12cm的同心圆扇形OCD所围成的(不计接缝)(如图1).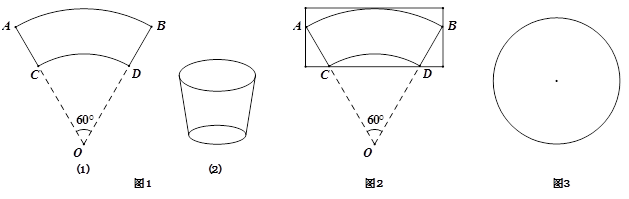
(1)求纸杯的底面半径和侧面积(结果保留π)
(2)要制作这样的纸杯侧面,如果按照图2所示的方式剪裁(不允许有拼接),至少要用多大的矩形纸片
(3)如图3,若在一张半径为18cm的圆形纸片上剪裁这样的纸杯侧面,最多能裁出多少个?
相关知识点
推荐套卷
某种规格小纸杯的侧面是由一半径为18cm、圆心角是60°的扇形OAB剪去一半径12cm的同心圆扇形OCD所围成的(不计接缝)(如图1).
(1)求纸杯的底面半径和侧面积(结果保留π)
(2)要制作这样的纸杯侧面,如果按照图2所示的方式剪裁(不允许有拼接),至少要用多大的矩形纸片
(3)如图3,若在一张半径为18cm的圆形纸片上剪裁这样的纸杯侧面,最多能裁出多少个?