已知双曲线W：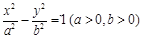
的左、右焦点分别为
、
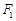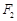，点
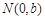，右顶点是M，且
，
．
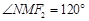（Ⅰ）求双曲线的方程；
（Ⅱ）过点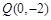
的直线l交双曲线W的右支于A、B两个不同的点（B在A、Q之间），若点
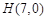在以线段AB为直径的圆的外部，试求△AQH与△BQH面积之比λ的取值范围．
棱柱中过侧棱的对角面的个数是
．
，是否存在
使等式
对
的一切自然数都成立，并证明你的结论．
和等比数列
，且
，
，
，
，
，试比较
与
，
与
的大小，并猜想
与
（
，
能被
整除（其中
）．
．相关知识点
推荐套卷
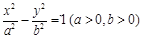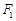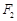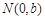已知双曲线W：的左、右焦点分别为、，点，右顶点是M，且，．
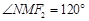（Ⅰ）求双曲线的方程；
（Ⅱ）过点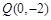的直线l交双曲线W的右支于A、B两个不同的点（B在A、Q之间），若点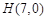在以线段AB为直径的圆的外部，试求△AQH与△BQH面积之比λ的取值范围．
粤公网安备 44130202000953号