）设点C为曲线y＝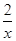
(x>0)上任一点，以点C为圆心的圆与x轴交于点E、A，与y轴交于点E、B.
(1)证明：多边形EACB的面积是定值，并求这个定值；
(2)设直线y＝－2x＋4与圆C交于点M，N，若|EM|＝|EN|，求圆C的方程．
,cosB=
, 试判断三角形的形状．
是同一三角形的两个内角，cos
=" -" 
,cos(
=-
.求cot
的值．
值相关知识点
推荐套卷
）设点C为曲线y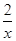＝(x>0)上任一点，以点C为圆心的圆与x轴交于点E、A，与y轴交于点E、B.
(1)证明：多边形EACB的面积是定值，并求这个定值；
(2)设直线y＝－2x＋4与圆C交于点M，N，若|EM|＝|EN|，求圆C的方程．
粤公网安备 44130202000953号