已知在数列{an}中，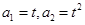
（t>0且t≠1）．
是函数
的一个极值点．
（1）证明数列
是等比数列，并求数列
的通项公式；
（2）记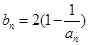
，当t=2时，数列
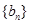的前n项和为Sn，求使Sn>2012的n的最小值；
（3）当t=2时，是否存在指数函数g（x），使得对于任意的正整数n有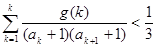
成立？若存在，求出满足条件的一个g（x）；若不存在，请说明理由．
相关试题
中，
分别为
中点．
平面
；
平面
．
，
是单位圆
上一动点，且点
的中点．
在
轴的正半轴上，求
；
，求点
到直线
的距离．
在
上是增函数，且
.
的取值范围；
在
上的最大值；
，
，求证：
．
满足
且在
时函数取得极值．
的值；
的单调区间；
上的最大值
的表达式．
满足
，
，
，
，
；
，并且用数学归纳法证明；
能被15整除．推荐套卷
已知在数列{an}中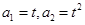，（t>0且t≠1）．是函数的一个极值点．
（1）证明数列是等比数列，并求数列的通项公式；
（2）记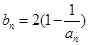，当t=2时，数列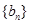的前n项和为Sn，求使Sn>2012的n的最小值；
（3）当t=2时，是否存在指数函数g（x），使得对于任意的正整数n有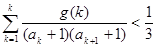成立？若存在，求出满足条件的一个g（x）；若不存在，请说明理由．
粤公网安备 44130202000953号