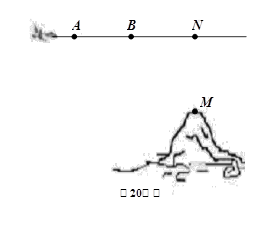
如图,飞机沿水平方向(A、B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低,就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行距离(因安全因素,飞机不能飞到山顶M的正上方N处才测飞行距离),请你设计一个求距离MN的方案,要求指出需要测量的数据(用字母表示,并在图中标出)
用你所设计测出的数据写出求距离MN的步骤
相关知识点
推荐套卷
如图,飞机沿水平方向(A、B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低,就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行距离(因安全因素,飞机不能飞到山顶M的正上方N处才测飞行距离),请你设计一个求距离MN的方案,要求指出需要测量的数据(用字母表示,并在图中标出)
用你所设计测出的数据写出求距离MN的步骤
