已知椭圆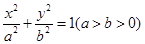 的左、右焦点分别是
的左、右焦点分别是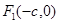 、
、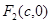 ,离心率为
,离心率为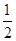 ,椭圆上的动点
,椭圆上的动点 到直线
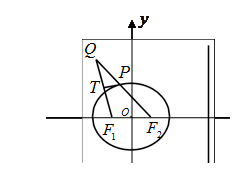
到直线 的最小距离为2,延长
的最小距离为2,延长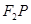 至
至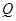 使得
使得 ,线段
,线段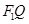 上存在异于
上存在异于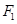 的点
的点 满足
满足 .
.
(1) 求椭圆的方程;
(2) 求点 的轨迹
的轨迹 的方程;
的方程;
(3) 求证:过直线 上任意一点必可以作两条直线
上任意一点必可以作两条直线
与 的轨迹
的轨迹 相切,并且过两切点的直线经过定点.
相切,并且过两切点的直线经过定点.
相关知识点
推荐套卷
已知椭圆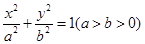 的左、右焦点分别是
的左、右焦点分别是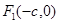 、
、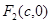 ,离心率为
,离心率为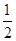 ,椭圆上的动点
,椭圆上的动点 到直线
到直线 的最小距离为2,延长
的最小距离为2,延长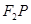 至
至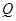 使得
使得 ,线段
,线段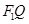 上存在异于
上存在异于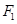 的点
的点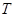 满足
满足 .
.
(1) 求椭圆的方程;
(2) 求点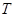 的轨迹
的轨迹 的方程;
的方程;
(3) 求证:过直线 上任意一点必可以作两条直线
上任意一点必可以作两条直线
与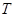 的轨迹
的轨迹 相切,并且过两切点的直线经过定点.
相切,并且过两切点的直线经过定点.