已知△ABC中，∠ACB=90°，AC=6，BC=8，过点A作直线MN⊥AC，点P是直线MN上的一个动点(与点A不重合)，连结CP交AB于点D，设AP=
，AD=
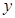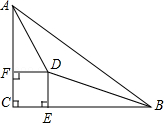
．如图1，若点P在射线AM上，求y与x的函数解析式；
射线AM上是否存在一点P，使以点D、A、P组成的三角形与△ABC相似，若存在，求AP的长，若不存在，说明理由；
如图2，过点B作BE⊥MN，垂足为E，以C为圆心、AC为半径的⊙C与以P为圆心PD为半径的动⊙P相切，求⊙P的半径
相关试题
中，
，
，
，求（1）
的值. 
中，
、
、
分别是
、AC、BC上的点，联结
、EF交于点G，且
.
相似的三角形（不用证明）；
，试求
的值．
. 求证：(1)
；(2) 
．
在平行四边形
的边
的延长线上，连结
交
于点
．求证：
.
相关知识点
推荐套卷
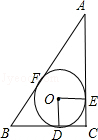
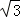粤公网安备 44130202000953号