已知A、D分别为椭圆E: 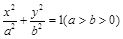 的左顶点与上顶点,椭圆的离心率
的左顶点与上顶点,椭圆的离心率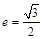 ,F1、F2为椭圆的左、右焦点,点P是线段AD上的任一点,且
,F1、F2为椭圆的左、右焦点,点P是线段AD上的任一点,且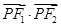 的最大值为1 .
的最大值为1 .
(1)求椭圆E的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且OA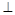 OB(O为坐标原点),若存在,求出该圆的方程;若不存在,请说明理由;
OB(O为坐标原点),若存在,求出该圆的方程;若不存在,请说明理由;
(3)设直线l与圆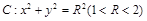 相切于A1,且l与椭圆E有且仅有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
相切于A1,且l与椭圆E有且仅有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
推荐套卷
已知A、D分别为椭圆E: 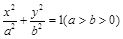 的左顶点与上顶点,椭圆的离心率
的左顶点与上顶点,椭圆的离心率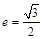 ,F1、F2为椭圆的左、右焦点,点P是线段AD上的任一点,且
,F1、F2为椭圆的左、右焦点,点P是线段AD上的任一点,且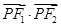 的最大值为1 .
的最大值为1 .
(1)求椭圆E的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且OA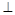 OB(O为坐标原点),若存在,求出该圆的方程;若不存在,请说明理由;
OB(O为坐标原点),若存在,求出该圆的方程;若不存在,请说明理由;
(3)设直线l与圆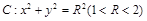 相切于A1,且l与椭圆E有且仅有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
相切于A1,且l与椭圆E有且仅有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.