已知函数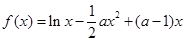 (
( 且
且 ).
).
(1)求函数 的单调区间;
的单调区间;
(2)记函数 的图象为曲线
的图象为曲线 .设点
.设点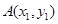 ,
, 是曲线
是曲线 上的不同两点.如果在曲线
上的不同两点.如果在曲线 上存在点
上存在点 ,使得:①
,使得:① ;②曲线
;②曲线 在点
在点 处的切线平行于直线
处的切线平行于直线 ,则称函数
,则称函数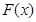 存在“中值相依切线”. 试问:函数
存在“中值相依切线”. 试问:函数 是否存在“中值相依切线”,请说明理由.
是否存在“中值相依切线”,请说明理由.
相关知识点
推荐套卷
已知函数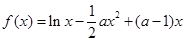 (
( 且
且 ).
).
(1)求函数 的单调区间;
的单调区间;
(2)记函数 的图象为曲线
的图象为曲线 .设点
.设点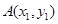 ,
, 是曲线
是曲线 上的不同两点.如果在曲线
上的不同两点.如果在曲线 上存在点
上存在点 ,使得:①
,使得:① ;②曲线
;②曲线 在点
在点 处的切线平行于直线
处的切线平行于直线 ,则称函数
,则称函数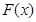 存在“中值相依切线”. 试问:函数
存在“中值相依切线”. 试问:函数 是否存在“中值相依切线”,请说明理由.
是否存在“中值相依切线”,请说明理由.