手工课时,小明准备做一个形状是菱形的风筝,这个菱形的两条对角线长度之和恰好为60 cm,菱形的面积S(单位:cm2)随其中一条对角线的长x(单位:cm)的变化而变化.请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
当x是多少时,菱形风筝面积S最大?最大面积是多少?______.
(参考公式:当x=-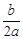 时,二次函数y=ax2+bx+c(a≠0)有最小(大)值
时,二次函数y=ax2+bx+c(a≠0)有最小(大)值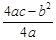 )
)
相关知识点
推荐套卷
手工课时,小明准备做一个形状是菱形的风筝,这个菱形的两条对角线长度之和恰好为60 cm,菱形的面积S(单位:cm2)随其中一条对角线的长x(单位:cm)的变化而变化.请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
当x是多少时,菱形风筝面积S最大?最大面积是多少?______.
(参考公式:当x=-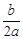 时,二次函数y=ax2+bx+c(a≠0)有最小(大)值
时,二次函数y=ax2+bx+c(a≠0)有最小(大)值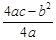 )
)