在平面直角坐标系xOy中，已知ΔPAB的顶点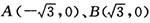
，P为动点，且
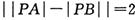.记动点P的轨迹为曲E
(I) 求曲线E的方程；
(II)设l是既不与AB平行也不与AB垂直的直线，且原点O到直线l的距离为
，l与曲线E相交于不同的两点G、H，问
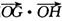的值是否为定值？若为定值，求出此定值；若不是，请说明理由.
相关试题
,若
.
的面积为
,求函数
的单调增区间
.
的最小正周期和值域;
为第二象限角，且
,求
的值.
在
处取得极值
.
;
为R上的奇函数,求函数
在区间
上的极值.
为平面向量,
.
的值;
,求实数
的值.
为圆
的直径，点
、
在圆
，矩形
所在的平面和圆
，
.
平面
；
的中点为
，求证：
平面
；
分成的两个锥体的体积分别为
，
，求
．推荐套卷
在平面直角坐标系xOy中，已知ΔPAB的顶点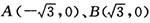，P为动点，且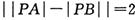.记动点P的轨迹为曲E
(I) 求曲线E的方程；
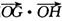(II)设l是既不与AB平行也不与AB垂直的直线，且原点O到直线l的距离为，l与曲线E相交于不同的两点G、H，问的值是否为定值？若为定值，求出此定值；若不是，请说明理由.
粤公网安备 44130202000953号