在海岸A处,发现北偏东 方向,距离A为
方向,距离A为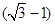 海里的B处有一走私船,在A北偏西
海里的B处有一走私船,在A北偏西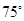 方向距离A为2海里的C处有我方一艘缉私艇奉命以
方向距离A为2海里的C处有我方一艘缉私艇奉命以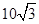 海里/小时的速度追截走私 船,且C在B的正西方,此时走私船正以
海里/小时的速度追截走私 船,且C在B的正西方,此时走私船正以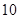 海里/小时的速度从B处向北偏东
海里/小时的速度从B处向北偏东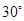 方向逃窜, 问缉私艇沿什么方向,才能最快追上走私船?需要多长时间?
方向逃窜, 问缉私艇沿什么方向,才能最快追上走私船?需要多长时间?
推荐套卷
在海岸A处,发现北偏东 方向,距离A为
方向,距离A为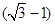 海里的B处有一走私船,在A北偏西
海里的B处有一走私船,在A北偏西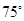 方向距离A为2海里的C处有我方一艘缉私艇奉命以
方向距离A为2海里的C处有我方一艘缉私艇奉命以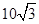 海里/小时的速度追截走私 船,且C在B的正西方,此时走私船正以
海里/小时的速度追截走私 船,且C在B的正西方,此时走私船正以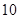 海里/小时的速度从B处向北偏东
海里/小时的速度从B处向北偏东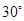 方向逃窜, 问缉私艇沿什么方向,才能最快追上走私船?需要多长时间?
方向逃窜, 问缉私艇沿什么方向,才能最快追上走私船?需要多长时间?