已知抛物线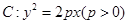
的焦点F和椭圆
的右焦点重合。
（1
）求抛物线C的方程，并求其准线方程；
（2）设P（1，2），是否存在平行于OP（O为坐标原点）的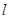直线
，使得直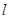线与抛物线
C有公共点，且直线OP与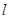的距离等于
？若存在，求出直线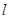的方程；若不存在，
说明理由。
相关试题
在其定义域
时单调递增, 且对任意的
都有
成立，且
,
的值;
.
的取值范围，使函数
在区间
上是单调函数;
, 记
, 求
的不等式: 
;
的值域, 并写出其单调区间.
,集合
.
,求实数
的取值范围; 
,求实数
，其中
．
的最大值和最小值；
满足：
恒成立，求相关知识点
推荐套卷
已知抛物线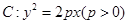的焦点F和椭圆的右焦点重合。
（1）求抛物线C的方程，并求其准线方程；
（2）设P（1，2），是否存在平行于OP（O为坐标原点）的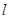直线，使得直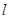线与抛物线
C有公共点，且直线OP与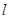的距离等于？若存在，求出直线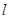的方程；若不存在，
说明理由。
粤公网安备 44130202000953号