某校为了更好地落实新课改,增加研究性学习的有效性,用分层抽样的方法从其中A、B、C三个学习小组中,抽取若干人进行调研,有关数据见下表(单位:人)
(1)求表中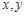 的值
的值
| 学习小组 |
小组人数 |
抽取人数 |
| A |
18 |
x |
| B |
36 |
2 |
| C |
54 |
y |
(2)若从B、C学习小组抽取的人中选2人作感想发言,求这2人都来自C学习小组的概率.
相关知识点
推荐套卷
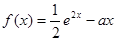 (
( ,
, 为自然对数的底数).
为自然对数的底数).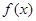 的单调性;
的单调性;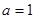 ,函数
,函数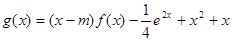 在区间
在区间 上为增函数,求整数
上为增函数,求整数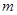 的最大值.
的最大值.
 的最小正周期和单调减区间;
的最小正周期和单调减区间;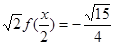 ,且
,且 ,求
,求 值.
值. (
( ).
). 时,求函数
时,求函数 在
在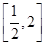 上的最大值和最小值;
上的最大值和最小值; 的取值范围.
的取值范围. (
( )在区间
)在区间 上有最大值
上有最大值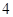 和最小值
和最小值 .设
.设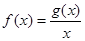 .
. 、
、 的值;
的值; 在
在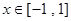 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.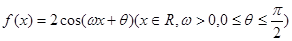 的图象与
的图象与 轴相交于点
轴相交于点 ,且该函数相邻两零点距离为
,且该函数相邻两零点距离为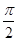 .
. 和
和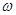 的值;
的值; ,
, ,求
,求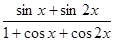 值.
值.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号