（本小题满分15分）如图，过抛物线
焦点F的直线l与抛物线交于A，B两点（A在第一象限），点C（0，t）（t>1）.
（I）若△CBF，△CFA，△CBA的面积成等差数列，求直线l的方程；
（II）若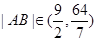
，且∠FAC为锐角，试求t的取值范围。
相关试题
满足
数列
的前n项和
的通项公式；
的前n项和
，函数
，
，
.
的单调递减区间；
上至少存在一个实数
，使
成立，试求正实数
的取值范围. 
为自然对数的底数，
的最小值；
图象的一个公共点坐标，并求它们在该公共点处的切线方程。
分别为三个内角A、B、C所对的边，
。 
的前
项和为
，
，满足
、
、
、
，并猜想推荐套卷
（本小题满分15分）如图，过抛物线焦点F的直线l与抛物线交于A，B两点（A在第一象限），点C（0，t）（t>1）.
（I）若△CBF，△CFA，△CBA的面积成等差数列，求直线l的方程；
（II）若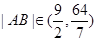，且∠FAC为锐角，试求t的取值范围。
粤公网安备 44130202000953号