在节能减排、保护地球环境的呼吁下,世界各国都很重视企业废水废气的排放处理。尽管企业对废水废气作了处理,但仍会对环境造成一些危害,所以企业在排出废水废气时要向当地居民支付一定的环境补偿费。已知某企业支付的环境补偿费P与该企业的废水排放量x满足关系式P=kx3(k∈[1,10]),具体k值由当地环保部门确定。而该企业的毛利润Q满足关系式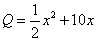 ,
,
(1)当k=1时,该企业为达到纯利润(Q-P)最大,废水排放量会达到多少?
(2)当x>1时,就会对居民健康构成危害。该地环保部门应在什么范围内设定k值,才能使该企业在达到最大利润时,废水排放量不会对当地居民健康构成危害?