如图所示，已知曲线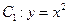
与曲线
交于点O、A，直线
(0<t≤1)与曲线C1、C2分别相交于点D、B，连接OD、DA、AB。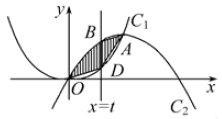
（1）写出曲边四边形ABOD（阴影部分）的面积S与t的函数关系式
；
（2）求函数在区间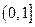
上的最大值。
相关试题
是递增的等差数列，
，求数列
的前n项和
．
，
，
．
的单调递增区间；
时，对任意
，不等式
恒成立，求实数的
取值范围．
的奇函数
．
；
，总有
，求实数
的取值范围．
，
．
时，求函数
的最小值；
恒成立，试求实数
中，
分别为
的对边,已知
．
；
，
时，求推荐套卷
如图所示，已知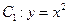曲线与曲线交于点O、A，直线(0<t≤1)与曲线C1、C2分别相交于点D、B，连接OD、DA、AB。
（1）写出曲边四边形ABOD（阴影部分）的面积S与t的函数关系式；
（2）求函数在区间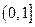上的最大值。
粤公网安备 44130202000953号