已知函数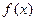 ,(
,( ),若同时满足以下条件:
),若同时满足以下条件:
①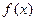 在D上单调递减或单调递增
在D上单调递减或单调递增
② 存在区间[ ]
] D,使
D,使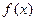 在[
在[ ]上的值域是[
]上的值域是[ ],那么称
],那么称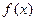 (
( )为闭函数。
)为闭函数。
(1)求闭函数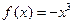 符合条件②的区间[
符合条件②的区间[ ];
];
(2)判断函数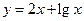 是不是闭函数?若是请找出区间[
是不是闭函数?若是请找出区间[ ];若不是请说明理由;
];若不是请说明理由;
(3)若 是闭函数,求实数
是闭函数,求实数 的取值范围.
的取值范围.
推荐套卷
已知函数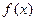 ,(
,( ),若同时满足以下条件:
),若同时满足以下条件:
①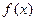 在D上单调递减或单调递增
在D上单调递减或单调递增
② 存在区间[ ]
] D,使
D,使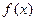 在[
在[ ]上的值域是[
]上的值域是[ ],那么称
],那么称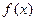 (
( )为闭函数。
)为闭函数。
(1)求闭函数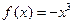 符合条件②的区间[
符合条件②的区间[ ];
];
(2)判断函数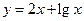 是不是闭函数?若是请找出区间[
是不是闭函数?若是请找出区间[ ];若不是请说明理由;
];若不是请说明理由;
(3)若 是闭函数,求实数
是闭函数,求实数 的取值范围.
的取值范围.