第11届全国人大五次会议于2012年3月5日至3月14日在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和14名记者担任对外翻译工作,调查发现,男、女记者中分别有10人和6人会俄语。
(I)根据以上数据完成以下2X2列联表: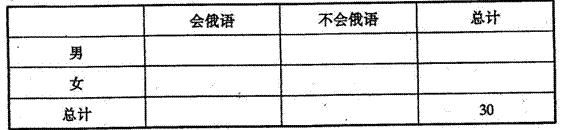
并回答能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?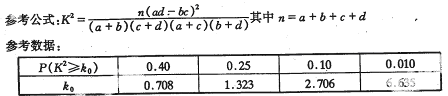
(II)会俄语的6名女记者中有4人曾在俄罗斯工作过,若从会俄语的6名女记者中随机抽
取2人做同声翻译,则抽出的2人都在俄罗斯工作过的概率是多少?
推荐套卷
第11届全国人大五次会议于2012年3月5日至3月14日在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和14名记者担任对外翻译工作,调查发现,男、女记者中分别有10人和6人会俄语。
(I)根据以上数据完成以下2X2列联表:
并回答能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?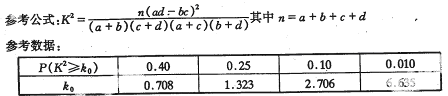
(II)会俄语的6名女记者中有4人曾在俄罗斯工作过,若从会俄语的6名女记者中随机抽
取2人做同声翻译,则抽出的2人都在俄罗斯工作过的概率是多少?