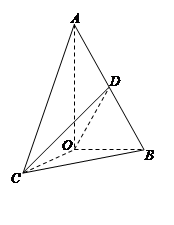如图，已知△AOB，∠AOB＝
，∠BAO＝
，AB＝4，D为线段AB的中点．若△AOC是△AOB绕直线AO旋转而成的．记二面角B－AO－C的大小为
．
（Ⅰ）当平面COD⊥平面AOB时，求的值；
（Ⅱ）当∈[，
]时，求二面角C－OD－B的余弦值的取值范围．
相关试题
的最大值。
(0≤θ<π)和
( t ∈R)，求它们的交点坐标．
的特征值
所对应的一个特征向量。
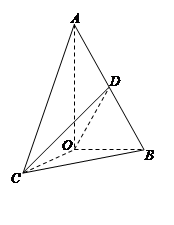
对应变换下变为点B(1，2)，求M－1.推荐套卷
如图，已知△AOB，∠AOB＝，∠BAO＝，AB＝4，D为线段AB的中点．若△AOC是△AOB绕直线AO旋转而成的．记二面角B－AO－C的大小为．
（Ⅰ）当平面COD⊥平面AOB时，求的值；
（Ⅱ）当∈[，]时，求二面角C－OD－B的余弦值的取值范围．
粤公网安备 44130202000953号