如图所示,⊙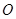 的直径
的直径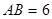 ,
,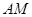 和
和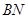 是它的两条切线,
是它的两条切线,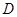 为射线
为射线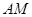 上的动点(不与
上的动点(不与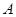 重合),
重合),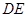 切⊙
切⊙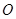 于
于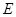 ,交
,交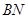 于
于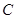 ,设
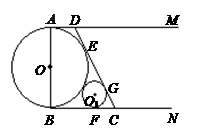
,设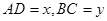 .
.
(1)求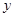 与
与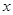 的函数关系式;
的函数关系式;
(2)若⊙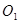 与⊙
与⊙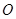 外切,且⊙
外切,且⊙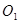 分别与
分别与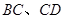
相切于点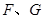 ,求
,求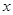 为何值时⊙
为何值时⊙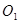 半径为1.
半径为1.
相关知识点
推荐套卷
如图所示,⊙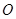 的直径
的直径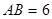 ,
,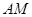 和
和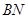 是它的两条切线,
是它的两条切线,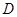 为射线
为射线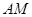 上的动点(不与
上的动点(不与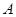 重合),
重合),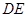 切⊙
切⊙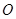 于
于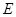 ,交
,交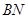 于
于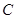 ,设
,设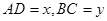 .
.
(1)求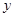 与
与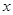 的函数关系式;
的函数关系式;
(2)若⊙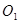 与⊙
与⊙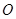 外切,且⊙
外切,且⊙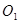 分别与
分别与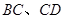
相切于点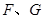 ,求
,求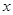 为何值时⊙
为何值时⊙ 半径为1.
半径为1.