（本小题满分8分）如图，抛物线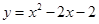
交x轴于A、B两点，顶点为C，经过A、B、C三点的圆的圆心为M.
⑴ 求圆心M的坐标；
⑵ 求⊙M上劣弧AB的长；
⑶ 在抛物线上是否存在一点D，使线段OC和MD互相平分？若存在，直接写出
点D的坐标，若不存在，请说明理由.
+|b3－27|=0，求(a－b)b的立方根.
相关知识点
推荐套卷
（本小题满分8分）如图，抛物线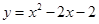交x轴于A、B两点，顶点为C，经过A、B、C三点的圆的圆心为M.
⑴ 求圆心M的坐标；
⑵ 求⊙M上劣弧AB的长；
⑶ 在抛物线上是否存在一点D，使线段OC和MD互相平分？若存在，直接写出点D的坐标，若不存在，请说明理由.
粤公网安备 44130202000953号